Dans la leçon précédente, nous avons vu combien il était compliqué d'essayer d'apprendre à Reeborg comment additionner deux nombres. Dans cette leçon, nous verrons combien il est facile de faire faire à Python des additions... et d'autres opérations mathématiques.
Selectionnez l'interpréteur Python (Python: Coder et Apprendre), en cliquant sur le troisième onglet. Votre affichage devrait ressembler à ce qui suit :
Ignorez les deux premières lignes de l'affichage pour l'instant. Sur la troisième ligne, il y a l'invite (ou prompt) de Python.
>>>
Maintenant, voyons si nous pouvons faire additionner deux nombres à Python plus facilement que Reeborg ne le pouvait. Mettez le pointeur sur la ligne 3, cliquez pour la sélectionner et tapez "Additionne 8 et 4" suivi de la touche "Entrée". Python va répondre, dans son propre langage, avec ce qui ressemble à des insultes !
>>>Additionne 8 et 4
File "<input>", line 1
Additionne 8 et 4
^
SyntaxError: invalid syntax
>>>
Ainsi, l'interpréteur Python ne comprend pas les commandes écrites en français. Essayons en anglais :
>>>Add 8 and 4
File "<input>", line 1
Add 8 and 4
^
SyntaxError: invalid syntax
>>>
Cela ne fonctionne pas non plus, mais vous avez dû remarquer que l'interpréteur reconnaît des mots-clés Python comme and puisqu'il les affiche dans une couleur différente de celle du reste du texte (aussi différente de la couleur que nous avons choisie mais cela n'a pas d'importance).
Remarquez qu'il vous invite encore une fois à lui donner une nouvelle entrée. Cette fois, essayez quelque chose de simple comme taper "8+4" suivi de la touche "Entrée". Vous devriez voir quelque chose comme ceci à l'affichage :
>>> 8+4
12
>>>
Gagné ! Python a additionné les deux nombres immédiatement (ce qui était si difficile à faire faire à Reeborg). Il vous invite même encore une fois à lui donner plus d'instructions. Vous pouvez essayer quelque chose comme ce qui suit (je l'ai copié de l'interpréteur).
>>> 8+4
12
>>> 8-4
4
>>> 8*4
32
>>> 8/4
2
Comme vous le voyez, Python sait additionner, soustraire, multiplier et diviser.
Python connaît l'ordre de priorité des opérateurs mathématiques. C'est ce qui fait que, quand vous avez plusieurs nombres et opérations mathématiques, vous multipliez et divisez les nombres d'abord (de gauche à droite), ensuite vous ajoutez et soustrayez, etc. Ici, quelques exemples donnent sans doute une meilleure explication que de simples mots :
>>> 2+3*5
17
>>> 2+ (3*5) # Python ne fait pas attention aux espaces ici
17
>>> (2+3)*5
25
>>> 2*4/8
1
>>> 2+1-4
-1
Allez-y, essayez quelques exemples de plus vous-même ! Voyez si vous pouvez parvenir à un résultat suprenant.
Si vous n'avez trouvé aucun résultat inattendu, c'est parce que vous n'avez pas essayé beaucoup d'exemples. Essayez par exemple 7/3. Comprenez-vous le résultat ? Essayez aussi 1/2.
Python reconnaît différents types de nombres. Le type le plus simple est celui des nombres entiers (en anglais integer). Quand Python divise un entier par un autre entier, il laisse tomber le reste de la division et ne nous donne qu'un nombre entier comme réponse. Donc, quand nous divisons 7 par 3 il nous donne 2 (le reste est 1). Pour obtenir le reste de la division, nous utilisons le symbole % :
>>> 7/3
2
>>> 7%3
1
>>> 1/2
0
>>> 1%2
1
Pour obtenir le résultat auquel nous nous attendions normalement, nous devons dire à Python d'utiliser des nombres réels ou flottants (en anglais floats). Nous faisons cela en ajoutant un point décimal à la fin d'au moins un des nombres.
[NdT : si en français les nombres décimaux (ou réels) se reconnaissent par leur virgule décimale (qui sépare la partie entière de la partie décimale), en anglais (et donc en Python) on utilise un point, comme avec la plupart des calculatrices]
>>> 1./2
0.5
>>> 1/2.
0.5
>>> 1.00000/2
0.5
Python en sait plus que les simples opérations mathématiques de base. Voici pour vous quelques exemples à essayer de développer.
>>> 3*3*3*3
81
>>> 3**4 # exponentiation (puissance)
81
>>> 7.3 % 3 # reste, encore une fois
1.2999999999999998
Ce dernier résultat est presque égal à 1,3 qui est le résultat que nous pouvions attendre. La différence entre 1,3 et 1,2999999999999998 est minuscule... Elle vient de la façon dont fonctionnent les ordinateurs quand ils traitent des fractions décimales. Je vous expliquerai cela dans une prochaine leçon, quand vous en saurez plus sur la programmation en général. Notez juste que, en pratique, une si petite différence entre le résultat "exact" et celui donné par Python (ou tout autre langage informatique) ne devrait pas avoir d'importance. Notez quand même qu'on peut faire afficher à Python les résultats d'une manière plus sensible ; essayez ce qui suit :
>>> print 7.3 % 3
1.3
Le mot-clé print commande à Python de nous montrer le résultat du calcul, et il le fait "intelligemment". Parfois, Python fera certains calculs sans afficher le résultat. En utilisant le mot-clé print, nous pouvons demander à Python d'afficher un résultat qui pourrait ne pas apparaître autrement.
Êtes-vous curieux ? Qu'arrive-t-il si vous mettez une instruction print dans un des programmes de Reeborg ?...
Essayez ce qui suit :
>>> 2147483647 + 1
2147483648L
Regardez bien : remarquez-vous le curieux "L" à la fin de la réponse ?
Il est là pour désigner ce qu'on appelle un entier Long,
c'est-à-dire un entier qui ne peut pas être facilement représenté dans
la mémoire d'un ordinateur. Pour un ordinateur avec ce qu'on appelle
une puce 32-bits, comme celui que j'utilise, et probablement vous
aussi, tous les nombres positifs sont représentés par diverses
combinaisons de 32 "bits", et l'entier le plus grand qui puisse donc
être représenté est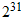 
-1 = 2147483647.
Tout entier plus grand que cela a besoin que Python (ou tout autre
langage informatique) utilise une technique avancée pour
effectuer des opérations mathématiques sur ces nombres. Cela ralentit
les calculs ; Python nous rappelle cela en marquant la lettre L à la
fin. À moins que vous n'en ayez vraiment besoin, évitez d'utiliser des
nombres extrêmement grands !
Essayez ce qui suit :
>>> 1,000
(1, 0)
>>> 1,000,000,000
(1, 0, 0, 0)
Que se passe-t-il ? Tout ce que je vous dirai pour l'instant, c'est que vous ne devez pas mettre de virgules dans les nombres pour séparer les milliers, comme cela se fait dans beaucoup de pays anglophones.
[NdT : Rappelez-vous que vous devrez remplacer la virgule décimale
que nous utilisons en français par un point pour séparer la partie
entière de la partie décimale d'un nombre. Ne séparez pas par contre
les milliers, millions et milliards.]
Nous verrons plus tard ce que signifient les virgules pour Python. Entre temps, nous pouvons voir ce que les virgules signifient quand nous les mettons dans une instruction print :
>>> print 5,4
5 4
>>> print 5, 4
5 4
Python considère que la virgule entre les deux nombres ci-dessus veut dire "mettre une seule espace entre les deux nombres (et ignorer toute autre espace en plus) au moment de les imprimer.
La notation scientifique vous est peut-être familière :
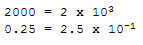
Si c'est le cas, vous savez que cette notation nous permet d'écrire des nombres extrêmement petits ou extrêmement grands d'une manière très commode. [Si vous ne connaissez pas la notation scientifique, vous pouvez sauter cette section puisque nous ne l'utiliserons pas dans la suite.] Python connaît également la notation scientifique mais il utilise la lettre E (ou e) pour représenter x 10
>>> 2e3
2000.0
>>> 2.5E-1
0.25
Essayez !
Python sait aussi manipuler les nombres complexes ainsi que les nombres en notations octale (base 8) et hexadécimale (base 16). Ne vous inquiétez pas si vous ne savez pas ce que c'est. Les seuls que nous aurons besoin d'utiliser sont les nombres hexadécimaux et nous donnerons des explications sur eux plus tard.
Python sait comparer des nombres et décider si l'un est plus petit que (<) l'autre, s'il est plus grand que (>) l'autre, s'ils sont égaux (==) ou s'ils ne sont pas égaux (!=).
[NdT : Python répond par True si c'est vrai ou False si c'est faux]
>>> 1<2
True
>>> 3<2
False
>>> 1>2
False
>>> 3>2
True
>>> 2==2
True
>>> 3==2
False
>>> 2!=2
False
>>> 3!=2
True
Essayez ! Notez bien l'utilisation de deux signes égal quand nous voulons tester si deux nombres sont égaux. Si vous utilisez un seul signe égal, Python se plaindra à sa façon [Il y a trois autres opérateurs de comparaison : <>, <=, >=. Vous pouvez les essayer et deviner ce qu'ils peuvent signifier].
Apprendre à Reeborg à faire des additions - 
- Interpréter les mots-clés Python.